



 2496 kB PostScript reprint
2496 kB PostScript reprint
Next: A Test for
Up: Data Modeling and
Previous: A Technique for
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
A. W. Jones, J. Bland-Hawthorn
Anglo-Australian Observatory, P.O. Box 296,
Epping, NSW 2121 Australia
P. L. Shopbell
Dept. of Space Physics & Astronomy, Rice University,
P.O. Box 1892,
Houston, TX 77251
Abstract:
Judged by their instrumental profiles, spectrometers fall into two
basic classes---Lorentzian and Gaussian---with many
other line profile functions (sinc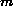 functions, Voigt functions, Airy functions, etc.) falling into one of
these two categories in some limit. We demonstrate that the Rayleigh,
Sparrow, and Houston resolution criteria are of limited use compared to
the ``equivalent width'' of the line profile.
functions, Voigt functions, Airy functions, etc.) falling into one of
these two categories in some limit. We demonstrate that the Rayleigh,
Sparrow, and Houston resolution criteria are of limited use compared to
the ``equivalent width'' of the line profile.
Modern day spectrographs ultimately rely on the interference of a
finite number of beams that traverse different optical paths to form a
signal (Bell 1972). The spectrometer disperses the incoming light into
a finite number of wavelength (energy) intervals, where the size of the
resolution element (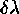 ) is set by the bandwidth limit
imposed by the dispersing element. Different dispersive techniques
produce a variety of instrumental profiles. A long-slit spectrometer in
the diffraction limit produces a
) is set by the bandwidth limit
imposed by the dispersing element. Different dispersive techniques
produce a variety of instrumental profiles. A long-slit spectrometer in
the diffraction limit produces a 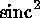 wavelength response, a
property shared with acousto-optic filters. In practice, optical and
mechanical defects within either device tend to make the instrumental
response more Gaussian in form. The response of the Fourier Transform
Spectrometer is fundamentally the
wavelength response, a
property shared with acousto-optic filters. In practice, optical and
mechanical defects within either device tend to make the instrumental
response more Gaussian in form. The response of the Fourier Transform
Spectrometer is fundamentally the 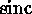 function,
although this response is commonly apodized to produce a profile with
better side-lobe behavior. An internally reflecting cavity (e.g.,
Fabry-Perot filter) generates an instrumental response given by the
periodic Airy function. In the limit of high finesse (the periodic
interval
function,
although this response is commonly apodized to produce a profile with
better side-lobe behavior. An internally reflecting cavity (e.g.,
Fabry-Perot filter) generates an instrumental response given by the
periodic Airy function. In the limit of high finesse (the periodic
interval  divided by the line FWHM
divided by the line FWHM 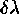 ),
the Airy function reduces to the Lorentzian function.
),
the Airy function reduces to the Lorentzian function.
The resolution element 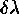 , or more formally the
spectral purity, is the smallest measurable wavelength difference at a
given wavelength
, or more formally the
spectral purity, is the smallest measurable wavelength difference at a
given wavelength 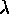 . In the case of rectangular and triangular
functions, the (average) instrumental width is unambiguous; for more
complex functions, a characteristic width can be more difficult to
define.
. In the case of rectangular and triangular
functions, the (average) instrumental width is unambiguous; for more
complex functions, a characteristic width can be more difficult to
define.
Rayleigh criterion. Lord Rayleigh (1879) first derived the
resolved distance of two identical, diffraction-limited point sources
with the aid of Bessel functions. This separation arises when the
peak of one Bessel function falls on the first zero point of the other
function. The often quoted resolution criterion, 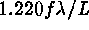 ,
where f is the focal ratio of the imaging system, was only
intended for use in this context. Thus, we do not investigate this
criterion further.
,
where f is the focal ratio of the imaging system, was only
intended for use in this context. Thus, we do not investigate this
criterion further.
Houston criterion. The usual metric in astronomy is to adopt the
``full width at half maximum'' (FWHM) as a suitable definition of
spectral purity 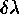 . Houston (1926) ventured that this
property can be used to define the natural separation of two identical
lines which are resolved from each other.
. Houston (1926) ventured that this
property can be used to define the natural separation of two identical
lines which are resolved from each other.
Sparrow criterion. Sparrow (1916) suggested a clever alternative,
which depends on the property of the summed line profiles. As we move
the lines closer together from far apart, a minimum develops. Sparrow
suggested that a natural definition for resolution results at the line
separation where the saddle point first develops (i.e., the gradient at
the peak of the summed profile is zero). More formally, for an
instrumental response given by 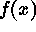 , then two sources are resolved at
a separation of
, then two sources are resolved at
a separation of 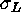 (Sparrow limit) when both of the following
conditions are satisfied:
(Sparrow limit) when both of the following
conditions are satisfied:
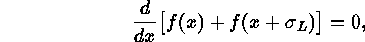
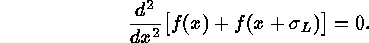
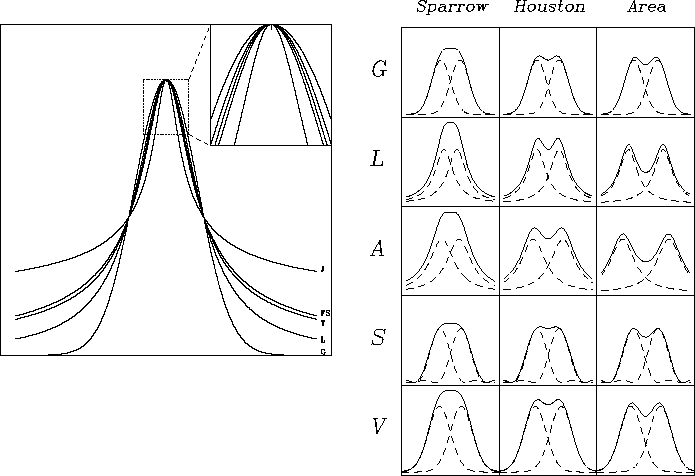
Figure: (a) Five functions with the same FWHM that demonstrate a
gradual trend in the ratio of core power to wing power: (G) Gaussian,
(L) Lorentzian, (T) 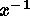 tanh x, (FS) Fraser-Suzuki function, (J)
the most extreme case to date discovered by AWJ. All of these functions
have continuous higher derivatives. In order for the function to remain
everywhere continuous, the neighborhood of the peak becomes narrower
(see inset) to compensate for the more extreme curvature near the
FWHM. (b) Three different possible criteria for the resolution of two
identical instrumental functions: (G) Gaussian, (L) Lorentzian, (A)
Airy, (S) sinc
tanh x, (FS) Fraser-Suzuki function, (J)
the most extreme case to date discovered by AWJ. All of these functions
have continuous higher derivatives. In order for the function to remain
everywhere continuous, the neighborhood of the peak becomes narrower
(see inset) to compensate for the more extreme curvature near the
FWHM. (b) Three different possible criteria for the resolution of two
identical instrumental functions: (G) Gaussian, (L) Lorentzian, (A)
Airy, (S) sinc , (V) Voigt.
Original PostScript figures
(2423 kB),
(45 kB)
, (V) Voigt.
Original PostScript figures
(2423 kB),
(45 kB)

Table: Resolution criteria for common spectral line functions in terms of the FWHM 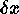 (see Figure 1). The
Airy function is periodic over the interval
(see Figure 1). The
Airy function is periodic over the interval 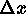 .
.
We illustrate a reductio ad absurdum arising from conventional
definitions of spectral resolution, with the aid of a series of
functions that are everywhere continuous and have the same FWHM, but have
varying core to wing ratios (see Figure 1(a)). Long-slit spectrometers
usually have rather Gaussian (G) profiles, whereas Fabry-Perot
interferometers approach Lorentzian (L) at high finesse. The extreme
wing-to-core ratio function (J) is not unlike the spatial
response function of the Hubble Space Telescope prior to installation
of the COSTAR optics. The Houston criterion implies that all of the
profiles have equal resolving ability. In contrast, the Sparrow
criterion would lead one to believe that narrow cores and large wings
have better resolution capabilities (see Table 1 and Figure 1(b)).
This is clearly not physical. A resolved core does not guarantee that
two profiles are clearly separated, since the wing contribution remains
unresolved. Intuitively, one way to see this is in terms of the shot
noise constraint. The uncertainty in finding the line centroid depends
inversely on the signal under the profile. As we
increase the wing power, for a constant line flux, the signal in the
core decreases dramatically.
In Table 1, we compare five different functional forms which arise in
observational astronomy. Each of the functions has been expressed in
terms of its FWHM 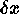 ; the Voigt function is expressed in two
different ways to emphasize its Lorentzian and Gaussian behavior in
the different limits. The various cases are illustrated in Figure 1(b).
The figure shows that the Sparrow criterion is the least
stringent, followed by the Houston criterion. The equivalent width
(area) criterion is least forgiving to the Lorentzian (and therefore
Airy) function. At first glance, it would appear that the Houston
criterion is sufficient to resolve two lines. However, to avoid the
logical dilemma described in the previous section, we should say that
the lines are properly resolved by the area criterion.
; the Voigt function is expressed in two
different ways to emphasize its Lorentzian and Gaussian behavior in
the different limits. The various cases are illustrated in Figure 1(b).
The figure shows that the Sparrow criterion is the least
stringent, followed by the Houston criterion. The equivalent width
(area) criterion is least forgiving to the Lorentzian (and therefore
Airy) function. At first glance, it would appear that the Houston
criterion is sufficient to resolve two lines. However, to avoid the
logical dilemma described in the previous section, we should say that
the lines are properly resolved by the area criterion.
We propose that the equivalent width (the area of the line profile
divided by the peak height) is a better measure of the spectral purity
of an instrumental function. This is more physical for a number of
reasons:
(1) the equivalent width, not the FWHM, constitutes the average width of the
profile,
(2) the equivalent width is more representative of the total signal under
the line profile,
(3) the equivalent width is a better discriminant of the wing behavior of a
line profile, and
(4) the equivalent width has an entirely general definition for an arbitrary
positive function.
For Gaussian
spectrometers (e.g., long-slit devices), the correction amounts to no
more than 6%. For Lorentzian spectrometers (e.g., Fabry-Perot
filters), this leads to a large correction factor (50--60%) to the
more standard use of the line profile FWHM.
Acknowledgments:
AWJ acknowledges a studentship (austral winter, 1994) at the Anglo-Australian Observatory.
References:
Bell, R. J. 1972, Introductory Fourier Transform
Spectroscopy (New York, Academic Press)
Fraser R. D. B., & Suzuki, E. 1969, Anal. Chem., 41, 37
Houston, W. V. 1926, ApJ, 64, 81
Rayleigh, Lord 1879, Phil. Mag., 8, 261
Sparrow, C. M. 1916, ApJ, 44, 76




 2496 kB PostScript reprint
2496 kB PostScript reprint
Next: A Test for
Up: Data Modeling and
Previous: A Technique for
adass4_editors@stsci.edu
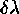 ) is set by the bandwidth limit
imposed by the dispersing element. Different dispersive techniques
produce a variety of instrumental profiles. A long-slit spectrometer in
the diffraction limit produces a
) is set by the bandwidth limit
imposed by the dispersing element. Different dispersive techniques
produce a variety of instrumental profiles. A long-slit spectrometer in
the diffraction limit produces a 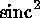 wavelength response, a
property shared with acousto-optic filters. In practice, optical and
mechanical defects within either device tend to make the instrumental
response more Gaussian in form. The response of the Fourier Transform
Spectrometer is fundamentally the
wavelength response, a
property shared with acousto-optic filters. In practice, optical and
mechanical defects within either device tend to make the instrumental
response more Gaussian in form. The response of the Fourier Transform
Spectrometer is fundamentally the 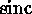 function,
although this response is commonly apodized to produce a profile with
better side-lobe behavior. An internally reflecting cavity (e.g.,
Fabry-Perot filter) generates an instrumental response given by the
periodic Airy function. In the limit of high finesse (the periodic
interval
function,
although this response is commonly apodized to produce a profile with
better side-lobe behavior. An internally reflecting cavity (e.g.,
Fabry-Perot filter) generates an instrumental response given by the
periodic Airy function. In the limit of high finesse (the periodic
interval  divided by the line FWHM
divided by the line FWHM 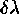 ),
the Airy function reduces to the Lorentzian function.
),
the Airy function reduces to the Lorentzian function.
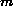 functions, Voigt functions, Airy functions, etc.) falling into one of
these two categories in some limit. We demonstrate that the Rayleigh,
Sparrow, and Houston resolution criteria are of limited use compared to
the ``equivalent width'' of the line profile.
functions, Voigt functions, Airy functions, etc.) falling into one of
these two categories in some limit. We demonstrate that the Rayleigh,
Sparrow, and Houston resolution criteria are of limited use compared to
the ``equivalent width'' of the line profile.
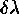 , or more formally the
spectral purity, is the smallest measurable wavelength difference at a
given wavelength
, or more formally the
spectral purity, is the smallest measurable wavelength difference at a
given wavelength 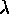 . In the case of rectangular and triangular
functions, the (average) instrumental width is unambiguous; for more
complex functions, a characteristic width can be more difficult to
define.
. In the case of rectangular and triangular
functions, the (average) instrumental width is unambiguous; for more
complex functions, a characteristic width can be more difficult to
define.
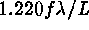 ,
where f is the focal ratio of the imaging system, was only
intended for use in this context. Thus, we do not investigate this
criterion further.
,
where f is the focal ratio of the imaging system, was only
intended for use in this context. Thus, we do not investigate this
criterion further.
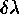 . Houston (1926) ventured that this
property can be used to define the natural separation of two identical
lines which are resolved from each other.
. Houston (1926) ventured that this
property can be used to define the natural separation of two identical
lines which are resolved from each other.
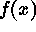 , then two sources are resolved at
a separation of
, then two sources are resolved at
a separation of 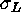 (Sparrow limit) when both of the following
conditions are satisfied:
(Sparrow limit) when both of the following
conditions are satisfied:
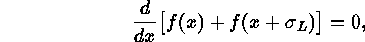
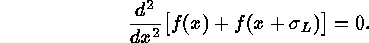

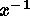 tanh x, (FS) Fraser-Suzuki function, (J)
the most extreme case to date discovered by AWJ. All of these functions
have continuous higher derivatives. In order for the function to remain
everywhere continuous, the neighborhood of the peak becomes narrower
(see inset) to compensate for the more extreme curvature near the
FWHM. (b) Three different possible criteria for the resolution of two
identical instrumental functions: (G) Gaussian, (L) Lorentzian, (A)
Airy, (S) sinc
tanh x, (FS) Fraser-Suzuki function, (J)
the most extreme case to date discovered by AWJ. All of these functions
have continuous higher derivatives. In order for the function to remain
everywhere continuous, the neighborhood of the peak becomes narrower
(see inset) to compensate for the more extreme curvature near the
FWHM. (b) Three different possible criteria for the resolution of two
identical instrumental functions: (G) Gaussian, (L) Lorentzian, (A)
Airy, (S) sinc , (V) Voigt.
Original PostScript figures
, (V) Voigt.
Original PostScript figures

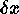 (see Figure 1). The
Airy function is periodic over the interval
(see Figure 1). The
Airy function is periodic over the interval 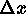 .
.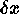 ; the Voigt function is expressed in two
different ways to emphasize its Lorentzian and Gaussian behavior in
the different limits. The various cases are illustrated in Figure 1(b).
The figure shows that the Sparrow criterion is the least
stringent, followed by the Houston criterion. The equivalent width
(area) criterion is least forgiving to the Lorentzian (and therefore
Airy) function. At first glance, it would appear that the Houston
criterion is sufficient to resolve two lines. However, to avoid the
logical dilemma described in the previous section, we should say that
the lines are properly resolved by the area criterion.
; the Voigt function is expressed in two
different ways to emphasize its Lorentzian and Gaussian behavior in
the different limits. The various cases are illustrated in Figure 1(b).
The figure shows that the Sparrow criterion is the least
stringent, followed by the Houston criterion. The equivalent width
(area) criterion is least forgiving to the Lorentzian (and therefore
Airy) function. At first glance, it would appear that the Houston
criterion is sufficient to resolve two lines. However, to avoid the
logical dilemma described in the previous section, we should say that
the lines are properly resolved by the area criterion.