



 600 kB PostScript reprint
600 kB PostScript reprint
Next: Clustering Analysis Algorithms
Up: Object Detection and
Previous: Unsupervised Catalog Classification
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
J.-L. Starck
CEA, DSM/DAPNIA, CEA-Saclay, F-91191 Gif-sur-Yvette Cedex, France
F. Murtagh
ST-ECF, ESO, Karl-Schwarzschild-Str. 2, D-85748 Garching, Germany
Affiliated to Astrophys. Div., Space Sci. Dept., ESA)
M. Louys
LSIT, ENSP, 7 rue de l'Université, F-67084 Strasbourg Cedex, France
Abstract:
We describe image compression based on the pyramidal median transform,
introduced as an alternative to the use of a wavelet transform.
The use of a multiresolution support allows ``protection'' of astronomical
objects in the image. Non-support parts of the images are subjected to
noise suppression. Experimental applications are presented.
Image compression is required for preview functionality in large image
databases (e.g., HST archive), for
linking image and catalog information in interactive sky atlases
(e.g., Aladin), and for image data transmission,
where more global views are communicated to the user, followed by more detail
if desired.
We describe an approach to astronomical image compression through noise
removal. Noise is determined on the basis of the image's assumed
stochastic properties.
This approach is quite similar to the wavelet transform-based hcompress
approach. We begin
by explaining why transforms other than the wavelet transform
are important for astronomical image compression.
Practical problems related to the use of the wavelet transform include:
- Negative Values.
- By definition, the wavelet coefficient mean is null. Every time we have
a positive structure at a scale, we have negative values surrounding it. These
negative values often create artifacts during the restoration process, or
complicate the analysis. For instance, if we threshold small values
(noise, non-significant structures, etc.) in the wavelet transform, and
then reconstruct the image at full resolution, the structure's flux
will be modified.
- Point Objects.
- We often have bright point objects in astronomical
images
(stars, cosmic ray hits, etc.), and the convolution of a Dirac
function with the wavelet transform is
equal to the wavelet transform. So at each scale, and at each point
source, we will have the wavelet. Cosmic rays can pollute all
the scales of the wavelet transform.
This leads us to develop other multiresolution tools which we now present.
The median transform is nonlinear, and offers advantages for robust
smoothing (i.e., the effects of outlier pixel values are mitigated).
The multiresolution median transform consists of a series of smoothings of
the input image, with successively broader kernels. Each successive
smoothing provides a new resolution scale.
The multiresolution coefficient values constructed by differencing
images at successive resolution scales are not necessarily of zero mean,
and so the potential artifact-creation difficulties related to
this aspect of wavelet transforms do not arise.
For integer input image values, this transform can be carried out in
integer arithmetic only, which may lead to computational savings.
Computational requirements of the multiresolution median transform are high,
and these can be reduced
by decimation: one pixel out of two is retained at each scale.
In the Pyramidal Median Transform (PMT),
the kernel or mask used to obtain the succession of resolution scales
remains the same at each level.
The image itself, to which this kernel is applied,
becomes smaller.
While this algorithm aids computationally, the reconstruction formula
for the input image is no longer immediate.
Instead, an algorithm based on B-spline interpolation can be used for
reconstruction.
An iterative scheme can be proposed for reconstructing an image, based
on pyramidal multi-median transform coefficients. Alternatively, the
PMT algorithm, itself, can be enhanced to
allow for better estimates of coefficient values,
yielding an Iterative Pyramidal Median Transform.
The principle of the method is to select the information we want to keep,
by using the PMT, and to code this information without any loss. Thus
the first phase searches for the minimum set of quantized multiresolution
coefficients which produce an image of ``high quality.'' The quality is
evidently subjective, and we will define by this term an image for
which
(1) there is no visual artifact in the decompressed image, and
(2) the residual (original image minus decompressed image) does not
contain any structure.
Lost information cannot be recovered, so if we do not accept any loss,
we have to compress what we take as
noise, too, and the compression ratio will be low (only 3 or 4).
The method employed involves the following sequence of operations:
- Determination of the multiresolution support.
- Determination of the quantized multiresolution coefficients which
gives the filtered image.
- Coding of each resolution level using the Huang-Bijaoui method (Huang
& Bijaoui 1991). This
consists of quadtree-coding each image, followed by Huffman-coding the
quadtree representation. There is no information lost during this phase.
- Compression of the noise, if this is desired.
- Decompression consists of reconstituting the noise-filtered image
(plus the compressed noise, if this was specified).
Note that we can reconstruct an image at a given resolution without having
to decode the entire compressed file.
A simulated HST WF/PC (pre-refurbishment) stellar field image
described in Hanisch (1993) was used. The image dimensions were
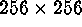 . Here we used the aberrated, noisy image.
With default options for the approach described in this
article ( pcomp/pdecomp; i.e., 5 iterations,
. Here we used the aberrated, noisy image.
With default options for the approach described in this
article ( pcomp/pdecomp; i.e., 5 iterations, 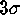 thresholding,
4 multiresolution scales, and no conservation of the noise)
a compressed image with 6643 bytes was obtained from the original image of
268,800 bytes. This is a compressed image equal to 2.5% of the original.
Even with I2 storage of the input image, we have compression to about 5%.
The total intensity dropped from 412,998 to 412,980 in compressing and
decompressing, i.e., a loss rate of 0.0044%.
thresholding,
4 multiresolution scales, and no conservation of the noise)
a compressed image with 6643 bytes was obtained from the original image of
268,800 bytes. This is a compressed image equal to 2.5% of the original.
Even with I2 storage of the input image, we have compression to about 5%.
The total intensity dropped from 412,998 to 412,980 in compressing and
decompressing, i.e., a loss rate of 0.0044%.
Using the known coordinate positions of the 470 stars in this image, we
obtained the intensities at these positions in the reconstructed image and
compared magnitudes in the
reconstructed image with magnitudes in the input image. There
was reasonable fidelity over about 8 magnitudes. For fainter objects, the
noise filtering causes greater difficulty, as one would expect.
The approach described here works well in practice. Further experiments
are described in the full paper.
Work comparing the approach described in this paper
with other well-known astronomical image
compression procedures is continuing.
References:

Figure: Difference between original and decompressed
image, using a stellar field.
Original PostScript figure (532 kB)
Hanisch, R., ed. 1993, Restoration---Newsletter of
ST ScI's Image Restoration Project (Baltimore, Space Telescope Science Institute)
Huang, L., & Bijaoui, A. 1991, Experimental Astronomy, 1, 311




 600 kB PostScript reprint
600 kB PostScript reprint
Next: Clustering Analysis Algorithms
Up: Object Detection and
Previous: Unsupervised Catalog Classification
adass4_editors@stsci.edu
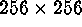 . Here we used the aberrated, noisy image.
With default options for the approach described in this
article ( pcomp/pdecomp; i.e., 5 iterations,
. Here we used the aberrated, noisy image.
With default options for the approach described in this
article ( pcomp/pdecomp; i.e., 5 iterations, 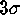 thresholding,
4 multiresolution scales, and no conservation of the noise)
a compressed image with 6643 bytes was obtained from the original image of
268,800 bytes. This is a compressed image equal to 2.5% of the original.
Even with I2 storage of the input image, we have compression to about 5%.
The total intensity dropped from 412,998 to 412,980 in compressing and
decompressing, i.e., a loss rate of 0.0044%.
thresholding,
4 multiresolution scales, and no conservation of the noise)
a compressed image with 6643 bytes was obtained from the original image of
268,800 bytes. This is a compressed image equal to 2.5% of the original.
Even with I2 storage of the input image, we have compression to about 5%.
The total intensity dropped from 412,998 to 412,980 in compressing and
decompressing, i.e., a loss rate of 0.0044%.
